In isotropic diffusion, the conductivity is adaptive to the local structure of the signal. But in comparison to anisotropic diffusion, the conductivity is still the same in all directions. Mathematically, the conductivity factor in the diffusion equation depends now on the signal \(u\) instead of being a constant
\begin{equation} \frac{\partial u(x,t)}{\partial t} = g(u(x, t)) \cdot \frac{\partial^2 u(x,t)}{\partial^2 x^2}. \label{eq:FEDIsotropic_PDE} \end{equation}In case of images and isotropic diffusion, the conductivity function may be related to the image gradient
\begin{equation} g(u(x, t)) = \frac{1}{\left(\frac{\left\| \nabla u(x,t) \right\|}{\lambda }\right)^2+1} \label{eq:FEDIsotropic_ConductivityFunction} \end{equation}with already a concrete function being used (more on this later) and where \(\lambda\) controls how strong the conductivity function reacts1. To use Fast Explicit Diffusion (FED) for isotropic problems the matrix \(A\) in
\begin{equation} \fvec{u}_{k+1} = \left( I + \tau \cdot A(\fvec{u}_k) \right) \cdot \fvec{u}_k \label{eq:FEDIsotropic_Discrete} \end{equation}now depends on the discrete signal vector \(\fvec{u}_k\)2 evolved to the diffusion time \(k\). To achieve isotropic diffusion in this scheme \(A(\fvec{u}_k)\) must somehow encode the information from \eqref{eq:FEDIsotropic_ConductivityFunction}. This article deals with this questions and gives a definition of \(A(\fvec{u}_k)\) like described in this paper.
Conductivity function
Before diving into the matrix definition, I first want to analyse the conductivity function from \eqref{eq:FEDIsotropic_ConductivityFunction} a bit more. Even though only this special definition of \(g(u(x, t))\) will be used here, let me note that others are possible, too (see e.g. Digital Image Processing by Burger and Burge, p. 437 for an overview) and which may behave slightly different.
So, what is the point of the conductivity function? Like in the homogeneous diffusion this parameter controls how fast the diffusion proceeds. But since \(g(u(x, t))\) now depends on the signal value this means that the diffusion behaves differently depending on the current structure described by the signal. E.g. if \(\fvec{u}\) describes an image diffusion means blurring an image and \(g(u(x, t))\) would make this blurring adaptive to the current image structure. More precisely, since the image gradient is used in \eqref{eq:FEDIsotropic_ConductivityFunction} this means that the blurring behaves differently at edges (high gradient magnitude) and homogeneous areas (low gradient magnitude). Often it is desired to suppress blurring around edges and enhance it in homogeneous areas3.
To achieve this behaviour, \(g(u(x, t))\) should return low values (resulting in low blurring) for higher gradient magnitudes and high values (resulting in high blurring) for lower gradient magnitudes. This is exactly the behaviour which is modelled by \eqref{eq:FEDIsotropic_ConductivityFunction}. The following animation shows this function with control over the parameter \(\lambda\) which scales the magnitude value. Larger \(\lambda\) means higher magnitude values conduct and get blurred as well; or in other words: more and more edges are included in the blurring process. One additional important note about this function is that it returns values in the range \(]0;1]\).
The goal is to define \(A(\fvec{u}_k)\) in a way that \eqref{eq:FEDIsotropic_Discrete} behaves as a good discretization of \eqref{eq:FEDIsotropic_PDE}. The first thing we do is that we apply the conductivity function in \eqref{eq:FEDIsotropic_ConductivityFunction} to all signal values
\begin{equation*} \fvec{g}_k = g(\fvec{u}_k). \end{equation*}These conductivity values will then later be used in \(A(\fvec{u}_k)\). Now, let me remind that \(A\) from the homogeneous diffusion process is defined to be an approximation of the second order derivative and each row can basically be seen as a discrete filter in the form \( \left( 1, -2, 1 \right) \), or equivalent: \( \left( 1, -(1+1), 1 \right) \). You can think of this as a weighted process which compares the centre element with its left neighbour by weighting the left side positive and the centre negative and analogous on the right side. \(A(\fvec{u}_k)\) should also encode this information somehow, but the weighting process will be a little bit more sophisticated. The idea is to define a filter like \( \left( a, -(a+b), b \right) \) with4
\begin{align*} a &= \frac{1}{2} \cdot \left( g_{i-1} + g_{i} \right) \\ b &= \frac{1}{2} \cdot \left( g_{i} + g_{i+1} \right) \end{align*}encoding the comparison process of the centre element \(i\) with its neighbours in a similar way as it was the case in the homogeneous diffusion, but rather using not only the signal values but the conductivity information instead. Here, the conductivity information is directly encoded with \(a\) being the average conductivity between the centre element and its left neighbour and \(b\) being the average conductivity between the centre element and its right neighbour.
Let's see how this filter expands for an \(i\) which is not the border element:
\begin{equation*} \begin{pmatrix} a \\ -(a+b) \\ b \\ \end{pmatrix} = \frac{1}{2} \cdot \begin{pmatrix} g_{i-1} + g_{i} \\ -(g_{i-1} + g_{i} + g_{i} + g_{i+1}) \\ g_{i} + g_{i+1} \\ \end{pmatrix} = \frac{1}{2} \cdot \begin{pmatrix} g_{i-1} + g_{i} \\ -g_{i-1} - 2\cdot g_{i} - g_{i+1} \\ g_{i} + g_{i+1} \\ \end{pmatrix} \end{equation*}As you can see, the weighting process is well defined since in total the elements sum up to zero. The next step is to use this pattern in the definition of \(A(\fvec{u}_k)\). Let's start with a one-dimensional signal vector.
1D example
I want to use a signal vector \(\fvec{u} \in \mathbb{R}^{9 \times 1}\) containing nine discrete elements. I don't use concrete values here because I think it won't be helpful for understanding the general computation pattern. Providing an example on the index level is more informative in my opinion. The reason for a \(9 \times 1\) vector lies in the fact that it is easily possible to use the same example later for the 2D case.
In this example, the matrix \(A(\fvec{u}_k)\) has the dimension \(9 \times 9\) and is defined as
\begin{equation*} A(\fvec{u}_k) = \frac{1}{2} \cdot \begin{pmatrix} -g_{0}-g_{1} & g_{0}+g_{1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ g_{0}+g_{1} & -g_{0}-2 g_{1}-g_{2} & g_{1}+g_{2} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & g_{1}+g_{2} & -g_{1}-2 g_{2}-g_{3} & g_{2}+g_{3} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & g_{2}+g_{3} & -g_{2}-2 g_{3}-g_{4} & g_{3}+g_{4} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & g_{3}+g_{4} & -g_{3}-2 g_{4}-g_{5} & g_{4}+g_{5} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & g_{4}+g_{5} & -g_{4}-2 g_{5}-g_{6} & g_{5}+g_{6} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & g_{5}+g_{6} & -g_{5}-2 g_{6}-g_{7} & g_{6}+g_{7} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & g_{6}+g_{7} & -g_{6}-2 g_{7}-g_{8} & g_{7}+g_{8} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & g_{7}+g_{8} & -g_{7}-g_{8} \\ \end{pmatrix} \end{equation*}Only the first and last row is a bit special since these are the border cases (signal values outside the border are set to zero). The rest of the matrix encodes the discussed weighting process between the centre element (diagonal components of the matrix) and its neighbours (left and right column of the diagonal components).
Remember that in \eqref{eq:FEDIsotropic_Discrete} the actual computation is \(A(\fvec{u}_k) \cdot \fvec{u}_k\), so the matrix must be multiplied with the signal vector. For the second row of \(A(\fvec{u}_k)\) this looks like
\begin{equation} \begin{split} \frac{1}{2} \cdot \begin{pmatrix} g_{0}+g_{1} & -g_{0}-2 g_{1}-g_{2} & g_{1}+g_{2} \\ \end{pmatrix} \cdot \begin{pmatrix} u_{0} \\ u_{1} \\ u_{2} \\ \end{pmatrix} = \\ \frac{1}{2} \cdot \left( (g_{0}+g_{1}) \cdot u_{0} + (-g_{0}-2 g_{1}-g_{2}) \cdot u_{1} + (g_{1}+g_{2}) \cdot u_{2} \right). \end{split} \label{eq:FEDIsotropic_1DComputationLine} \end{equation}In total, this results in
\begin{equation*} A(\fvec{u}_k) \cdot \fvec{u}_k = \frac{1}{2} \cdot \begin{pmatrix} \left(-g_{0}-g_{1}\right) u_{0}+\left(g_{0}+g_{1}\right) u_{1} \\ \left(g_{0}+g_{1}\right) u_{0}+\left(-g_{0}-2 g_{1}-g_{2}\right) u_{1}+\left(g_{1}+g_{2}\right) u_{2} \\ \left(g_{1}+g_{2}\right) u_{1}+\left(-g_{1}-2 g_{2}-g_{3}\right) u_{2}+\left(g_{2}+g_{3}\right) u_{3} \\ \left(g_{2}+g_{3}\right) u_{2}+\left(-g_{2}-2 g_{3}-g_{4}\right) u_{3}+\left(g_{3}+g_{4}\right) u_{4} \\ \left(g_{3}+g_{4}\right) u_{3}+\left(-g_{3}-2 g_{4}-g_{5}\right) u_{4}+\left(g_{4}+g_{5}\right) u_{5} \\ \left(g_{4}+g_{5}\right) u_{4}+\left(-g_{4}-2 g_{5}-g_{6}\right) u_{5}+\left(g_{5}+g_{6}\right) u_{6} \\ \left(g_{5}+g_{6}\right) u_{5}+\left(-g_{5}-2 g_{6}-g_{7}\right) u_{6}+\left(g_{6}+g_{7}\right) u_{7} \\ \left(g_{6}+g_{7}\right) u_{6}+\left(-g_{6}-2 g_{7}-g_{8}\right) u_{7}+\left(g_{7}+g_{8}\right) u_{8} \\ \left(g_{7}+g_{8}\right) u_{7}+\left(-g_{7}-g_{8}\right) u_{8} \\ \end{pmatrix} \end{equation*}If we would use this in real applications, we would not really set up the matrix \( A(\fvec{u}_k) \) and perform matrix multiplication. The matrix is way to sparse (containing too many zero elements) in order to make this computational efficient. Instead, it is more efficient to focus on the computation in \eqref{eq:FEDIsotropic_1DComputationLine} and abstract from that. If you look close, you see that the computation consists of six additions/subtractions and three multiplications. With a little bit of restructuring
\begin{align*} &(g_{0}+g_{1}) \cdot u_{0} + (-g_{0}-2 g_{1}-g_{2}) \cdot u_{1} + (g_{1}+g_{2}) \cdot u_{2} \\ &= (g_{0}+g_{1}) \cdot u_{0} + (-g_{0}-g_{1}) \cdot u_{1} + (-g_{1}-g_{2}) \cdot u_{1} + (g_{1}+g_{2}) \cdot u_{2} \\ &= (g_{0}+g_{1}) \cdot u_{0} - (g_{0}+g_{1}) \cdot u_{1} - (g_{1}+g_{2}) \cdot u_{1} + (g_{1}+g_{2}) \cdot u_{2} \\ &= (g_{0}+g_{1}) \cdot (u_{0} - u_{1}) + (g_{1}+g_{2}) \cdot (u_{2} - u_{1}) \end{align*}we only have 5 additions/subtractions and 2 multiplications left. The following figure depicts the general computation pattern.
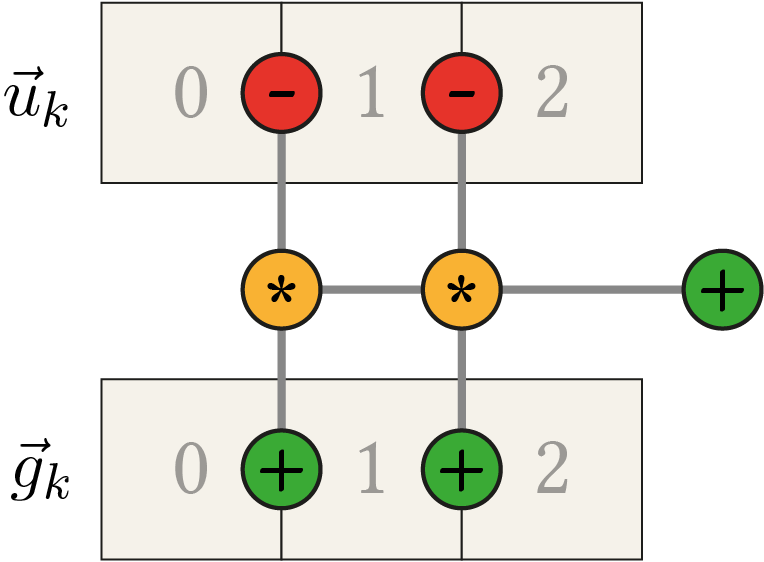
Remember that in order to calculate \(\tau_i\) in the FED scheme (\eqref{eq:FEDIsotropic_Discrete}) the maximum step size \(\tau_{\text{max}}\) which is still stable in the explicit scheme is needed and can be approximated by the maximum eigenvalue of \(A(\fvec{u}_k)\). Since the maximum return value of \(g(u(x,t))\) is 1 we now know that a row of \(A(\fvec{u}_k)\) has the values \( 0.5 \cdot \left( 2, -4, 2 \right) \) in the extreme case resulting in a maximum absolute eigenvalue of 4, hence \(\tau_{\text{max}} = 0.25\) can be used5.
2D example
Adding an additional dimension to the diffusion process basically means that the second order derivative now needs to be approximated in two directions: \(A_x(\fvec{u}_k)\) for the horizontal and \(A_y(\fvec{u}_k)\) for the vertical direction. Both matrices are additively combined, meaning the FED scheme from \eqref{eq:FEDIsotropic_Discrete} changes to
\begin{equation} \fvec{u}_{k+1} = \left( I + \tau_i \cdot \left( A_x(\fvec{u}_k) + A_y(\fvec{u}_k) \right) \right) \cdot \fvec{u}_k. \label{eq:FEDIsotropic_2DDiscrete} \end{equation}Unfortunately, the second dimension brings also more effort for the border handling since more border accesses need to be considered. As an example, I want to analyse the \(3 \times 3 \) image
\begin{equation*} \fvec{u} = \begin{pmatrix} u_{0} & u_{1} & u_{2} \\ u_{3} & u_{4} & u_{5} \\ u_{6} & u_{7} & u_{8} \\ \end{pmatrix}. \end{equation*}In the \(x\)-dimension only the vector components \(u_{1}, u_{4}\) and \(u_{7}\) are inside of the matrix, respectively the components \(u_{3}, u_{4}\) and \(u_{5}\) in the \(y\)-dimension. But this is only so drastic because the example is very small. If the matrix is larger (e.g. represents an image) the border cases may be negligible. To apply the matrices \(A_x(\fvec{u}_k)\) and \(A_y(\fvec{u}_k)\) in a similar way, as it was the case in the 1D example, we assume that the signal matrix is reshaped to a one-dimensional vector. This allows us to use similar computations as in the 1D example. First the definition of
\begin{equation*} A_x(\fvec{u}_k) = \frac{1}{2} \cdot \begin{pmatrix} -g_{0}-g_{1} &g_{0}+g_{1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ g_{0}+g_{1} & -g_{0}-2g_{1}-g_{2} &g_{1}+g_{2} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 &g_{1}+g_{2} & -g_{1}-g_{2} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -g_{3}-g_{4} &g_{3}+g_{4} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 &g_{3}+g_{4} & -g_{3}-2g_{4}-g_{5} &g_{4}+g_{5} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 &g_{4}+g_{5} & -g_{4}-g_{5} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & -g_{6}-g_{7} &g_{6}+g_{7} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 &g_{6}+g_{7} & -g_{6}-2g_{7}-g_{8} &g_{7}+g_{8} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 &g_{7}+g_{8} & -g_{7}-g_{8} \\ \end{pmatrix} \end{equation*}which now includes two more border cases (third and sixth row) but otherwise did not changed from the 1D case. The calculation in \eqref{eq:FEDIsotropic_2DDiscrete} is easiest done if \(A_x(\fvec{u}_k) \cdot \fvec{u}_k\) and \(A_y(\fvec{u}_k) \cdot \fvec{u}_k\) are applied separately. For the first matrix, this results in
\begin{equation*} A_x(\fvec{u}_k) \cdot \fvec{u}_k = \frac{1}{2} \cdot \begin{pmatrix} \left(-g_{0}-g_{1}\right) u_0+\left(g_{0}+g_{1}\right) u_1 \\ \left(g_{0}+g_{1}\right) u_0+\left(-g_{0}-2 g_{1}-g_{2}\right) u_1+\left(g_{1}+g_{2}\right) u_2 \\ \left(g_{1}+g_{2}\right) u_1+\left(-g_{1}-g_{2}\right) u_2 \\ \left(-g_{3}-g_{4}\right) u_3+\left(g_{3}+g_{4}\right) u_4 \\ \left(g_{3}+g_{4}\right) u_3+\left(-g_{3}-2 g_{4}-g_{5}\right) u_4+\left(g_{4}+g_{5}\right) u_5 \\ \left(g_{4}+g_{5}\right) u_4+\left(-g_{4}-g_{5}\right) u_5 \\ \left(-g_{6}-g_{7}\right) u_6+\left(g_{6}+g_{7}\right) u_7 \\ \left(g_{6}+g_{7}\right) u_6+\left(-g_{6}-2 g_{7}-g_{8}\right) u_7+\left(g_{7}+g_{8}\right) u_8 \\ \left(g_{7}+g_{8}\right) u_7+\left(-g_{7}-g_{8}\right) u_8 \\ \end{pmatrix} \end{equation*}and reveals a very similar computation pattern as in the 1D case. For the \(y\)-dimension the matrix is defined as
\begin{equation*} A_y(\fvec{u}_k) = \frac{1}{2} \cdot \begin{pmatrix} -g_{0}-g_{3} & 0 & 0 & g_{0}+g_{3} & 0 & 0 & 0 & 0 & 0 \\ 0 & -g_{1}-g_{4} & 0 & 0 & g_{1}+g_{4} & 0 & 0 & 0 & 0 \\ 0 & 0 & -g_{2}-g_{5} & 0 & 0 & g_{2}+g_{5} & 0 & 0 & 0 \\ g_{0}+g_{3} & 0 & 0 & -g_{0}-2 g_{3}-g_{6} & 0 & 0 & g_{3}+g_{6} & 0 & 0 \\ 0 & g_{1}+g_{4} & 0 & 0 & -g_{1}-2 g_{4}-g_{7} & 0 & 0 & g_{4}+g_{7} & 0 \\ 0 & 0 & g_{2}+g_{5} & 0 & 0 & -g_{2}-2 g_{5}-g_{8} & 0 & 0 & g_{5}+g_{8} \\ 0 & 0 & 0 & g_{3}+g_{6} & 0 & 0 & -g_{3}-g_{6} & 0 & 0 \\ 0 & 0 & 0 & 0 & g_{4}+g_{7} & 0 & 0 & -g_{4}-g_{7} & 0 \\ 0 & 0 & 0 & 0 & 0 & g_{5}+g_{8} & 0 & 0 & -g_{5}-g_{8} \\ \end{pmatrix} \end{equation*}which looks very different at the first glance. But the computation is actually the same, we only need to combine elements vertically now, e.g. \(u_{0}\) (first row) and \(u_{3}\) (fourth row), and the reshaped signal value offers no consecutive access here. For the combination with the signal vector as implied by \eqref{eq:FEDIsotropic_2DDiscrete} we get
\begin{equation*} A_y(\fvec{u}_k) \cdot \fvec{u}_k = \frac{1}{2} \cdot \begin{pmatrix} \left(-g_{0}-g_{3}\right) u_{0}+\left(g_{0}+g_{3}\right) u_{3} \\ \left(-g_{1}-g_{4}\right) u_{1}+\left(g_{1}+g_{4}\right) u_{4} \\ \left(-g_{2}-g_{5}\right) u_{2}+\left(g_{2}+g_{5}\right) u_{5} \\ \left(g_{0}+g_{3}\right) u_{0}+\left(-g_{0}-2 g_{3}-g_{6}\right) u_{3}+\left(g_{3}+g_{6}\right) u_{6} \\ \left(g_{1}+g_{4}\right) u_{1}+\left(-g_{1}-2 g_{4}-g_{7}\right) u_{4}+\left(g_{4}+g_{7}\right) u_{7} \\ \left(g_{2}+g_{5}\right) u_{2}+\left(-g_{2}-2 g_{5}-g_{8}\right) u_{5}+\left(g_{5}+g_{8}\right) u_{8} \\ \left(g_{3}+g_{6}\right) u_{3}+\left(-g_{3}-g_{6}\right) u_{6} \\ \left(g_{4}+g_{7}\right) u_{4}+\left(-g_{4}-g_{7}\right) u_{7} \\ \left(g_{5}+g_{8}\right) u_{5}+\left(-g_{5}-g_{8}\right) u_{8} \\ \end{pmatrix} \end{equation*}Note how e.g. the middle line combines \(u_{1}\) (top) with \(u_{4}\) (middle) and \(u_{7}\) (bottom) and how these elements are aligned vertically in the signal matrix \(\fvec{u}\). Like in the 1D case, it is possible to optimize the computation for a matrix line, e.g. for the middle line in \(A_y(\fvec{u}_k) \cdot \fvec{u}_k\)
\begin{align*} & \left(g_{1}+g_{4}\right) \cdot u_{1} + \left(-g_{1}-2 g_{4}-g_{7}\right) \cdot u_{4} +\left(g_{4}+g_{7}\right) \cdot u_{7} \\ &= \left(g_{1}+g_{4}\right) \cdot u_{1} - \left(g_{1}+g_{4}\right) \cdot u_{4} - \left(g_{4} + g_{7}\right) \cdot u_{4} +\left(g_{4}+g_{7}\right) \cdot u_{7} \\ &= \left(g_{1}+g_{4}\right) \cdot \left( u_{1} - u_{4}\right) +\left(g_{4}+g_{7}\right) \cdot \left( u_{7} - u_{4} \right). \\ \end{align*}The optimization alongside the \(x\)-direction can directly be copied from the 1D case. To sum up, the following figure illustrates the general computation pattern for the 2D case.
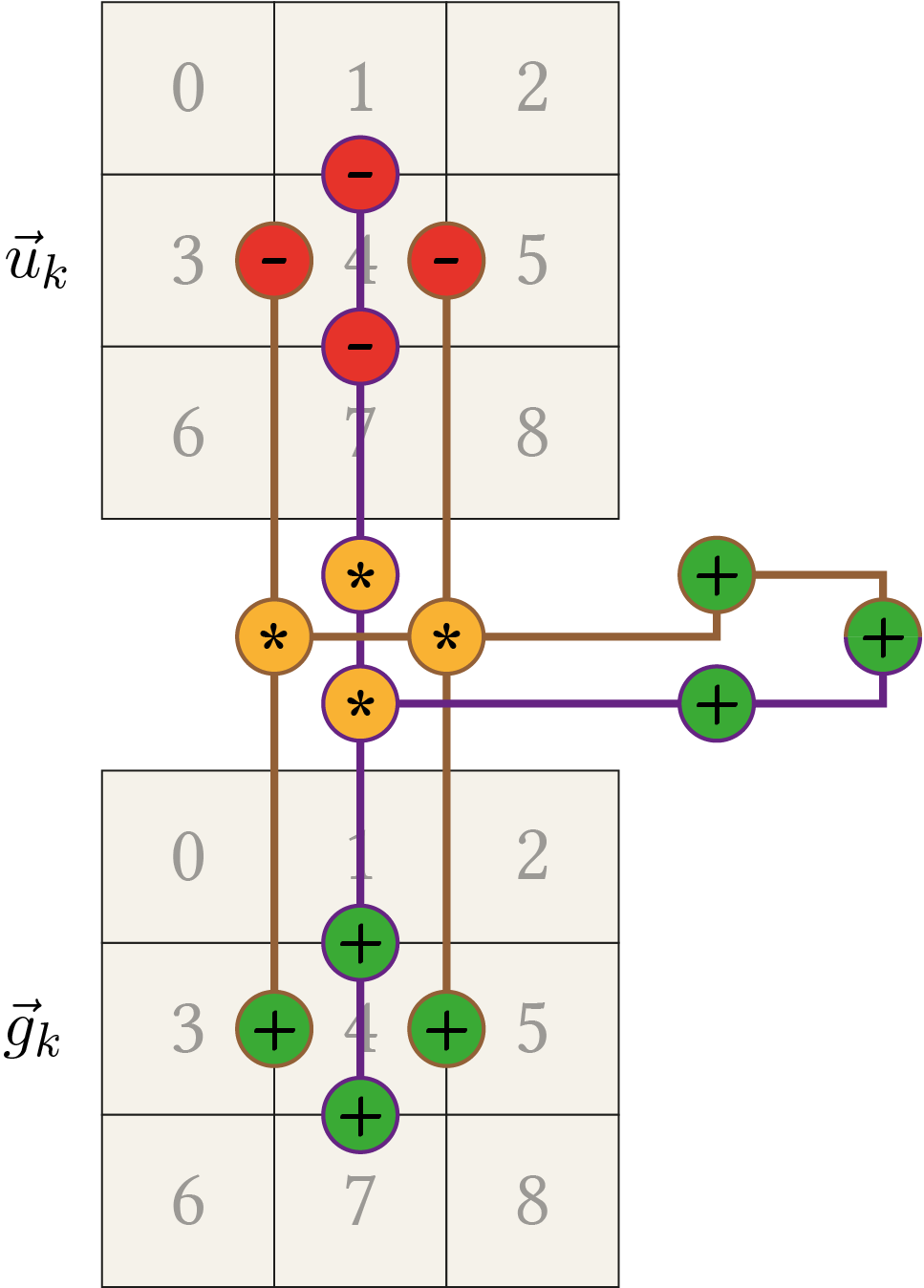
You can move this pattern around to any image location. If some of the computations touch the border, this part is set to zero. E.g. when centred around the element with index 3, the left subtraction/addition is neglected. This is in agreement with the definition of \(A(\fvec{u}_k)\) where the computation is also reduced if out of border values are involved.
Given all this, it is relatively straightforward to implement a FED step (one iteration of a FED cycle). The following listing shows an example implementation in C++ using the OpenCV library6. The function takes the image from the previous iteration, the conductivity image for the current FED cycle (the conductivity image only changes after the FED cycle completes) and the current step size as input. The full source code is available on GitHub.
static cv::Mat FEDInnerStep(const cv::Mat& img, const cv::Mat& cond, const double stepsize)
{
// Copy input signal vector
cv::Mat imgCopy = img.clone();
// Apply the computation pattern to each image location
for (int row = 0; row < img.rows; row++)
{
for (int col = 0; col < img.cols; col++)
{
double xLeft = 0;
double xRight = 0;
double yTop = 0;
double yBottom = 0;
if (col > 0)
{
// 3 <--> 4
xLeft = (cond.at<double>(row, col - 1) + cond.at<double>(row, col)) * (img.at<double>(row, col - 1) - img.at<double>(row, col));
}
if (col < img.cols - 1)
{
// 4 <--> 5
xRight = (cond.at<double>(row, col) + cond.at<double>(row, col + 1)) * (img.at<double>(row, col + 1) - img.at<double>(row, col));
}
if (row > 0)
{
// 1 <--> 4
yTop = (cond.at<double>(row - 1, col) + cond.at<double>(row, col)) * (img.at<double>(row - 1, col) - img.at<double>(row, col));
}
if (row < img.rows - 1)
{
// 4 <--> 7
yBottom = (cond.at<double>(row, col) + cond.at<double>(row + 1, col)) * (img.at<double>(row + 1, col) - img.at<double>(row, col));
}
// Update the current pixel location with the conductivity based derivative information and the varying step size
imgCopy.at<double>(row, col) = 0.5 * stepsize * (xLeft + xRight + yTop + yBottom);
}
}
// Update old image
return img + imgCopy;
}
Note that this is basically the computation pattern from the figures with some additional logic for the border handling. If you have read my article about FED, you might have been a bit disappointed that no real application was shown. But without a definition of the conductivity matrix, it is hard to show something useful. Nevertheless, we have now all ingredients together so that it is possible to apply isotropic diffusion to an example image. The following animation lets you control this process starting from \(T=0\) (original image) up to the diffusion time \(T=100\). If you switch to the right tab, you can see the result of the corresponding homogeneous diffusion process (applied via Gaussian convolution).
As you can see, the isotropic diffusion results in blurred regions but the main edges stay intact. E.g. the fine left background structure is nearly completely lost at the end but the stripes of the clothes are still visible. This effect is especially noticeable when the result is compared with the Gaussian filter response, which blurs everything equally regardless of its content.
List of attached files:
- FEDIsotropic_ConductivityFunction.nb [PDF] (Mathematica notebook used to plot the conductivity function in \eqref{eq:FEDIsotropic_ConductivityFunction})
- FEDIsotropic_ConductivityMatrix.nb [PDF] (Mathematica notebook containing the matrix calculations)